Robustness of the 2.11 Sharpe Mean Reversion Strategy

Reaching 26% annual returns by trading multiple instruments in parallel

The Death of Socrates, 1787, by Jacques Louis David

The idea

“As for me, all I know is that I know nothing.” Socrates.

I love this quote. Humility is such an important virtue, especially in trading. If someone already knows something, their curiosity is gone. Their desire to learn is weak or non-existent.

After I published the first article, some people questioned the strategy's robustness. Some affirmed, just by looking at the equity curve, that the system was overfitted. Although I would rather test a new system (I have over a hundred ideas in the backlog and am growing), I'm curious to answer the question some people asked: Is the first strategy we published robust, or is it overfitted?

So, this week, let's review the robustness of the first strategy published. Remembering the rules:

• Compute the rolling mean of High minus Low over the last 25 days;

• Compute the IBS indicator: (Close - Low) / (High - Low);

• Compute a lower band as the rolling High over the last 10 days minus 2.5 x the rolling mean of High mins Low (first bullet);

• Go long whenever SPY closes under the lower band (3rd bullet) and IBS is lower than 0.3;

• Close the trade whenever the SPY close is higher than yesterday's high;

• Also, close the trade whenever the price is lower than the 300-SMA.

Here's the study plan:

1. First, we will explore the parameter space by running 1,875 experiments varying the parameters for the strategy applied to QQQ;

2. Then, we will investigate the statistical properties of the edge, looking into all events not only for QQQ but for all +21K stocks (listed and delisted) since 1998;

3. Finally, we will try to improve the strategy by trading several instruments in parallel instead of just one (QQQ).

Sensitivity analysis for the original strategy

Let's start by exploring the parameter space. We will run 1,875 experiments. The parameters to be tried:

• 25 days: [23, 24, 25, 26, 27]

• 10 days: [8, 9, 10, 11, 12]

• 2.5x (lower band): [2.3, 2.4, 2.5, 2.6, 2.7]

• 0.30 IBS threshold: [0.28, 0.29, 0.30, 0.31, 0.32]

• 300-day SMA: [280, 300, 320]

Let's see the results:

Equity curve, drawdown curve, and annual returns for the enhanced strategy 1,875 variations

Statistics for the main indicators of the 1,875 experiments

Contrary to what some people said, the data suggests the strategy is robust indeed and not overfitted to a specific choice of parameters.

However, instead of expecting a 2.11 Sharpe, after running these ~2K experiments, I'd expect a lower value (1.95-1.99).

Also, although robust, the mean annual return of the 1,875 experiments is only 11.8%. Yes, it is slightly above the 10.0% annual return of the benchmark in the period (buy & hold QQQ). However, the strategy underperformed the benchmark in 7 out of the last 10 years. This is not ideal.

Let's see if we can improve that. The idea is to increase the exposure time by trading multiple assets in parallel.

The edge

Let's start by investigating the edge of these strategy's rules. What would have happened if we had bought all events when a stock closed lower than the lower band and its IBS was below 0.3 and held it for 5 days? As we are looking now to individual stocks instead of broad indices, we added 2 additional conditions:

• Stocks must have a close price above $10 at the beginning of the trade;

• Stocks must have a close price above their 200-day moving average.

Here are the stats:

Statistics of the events

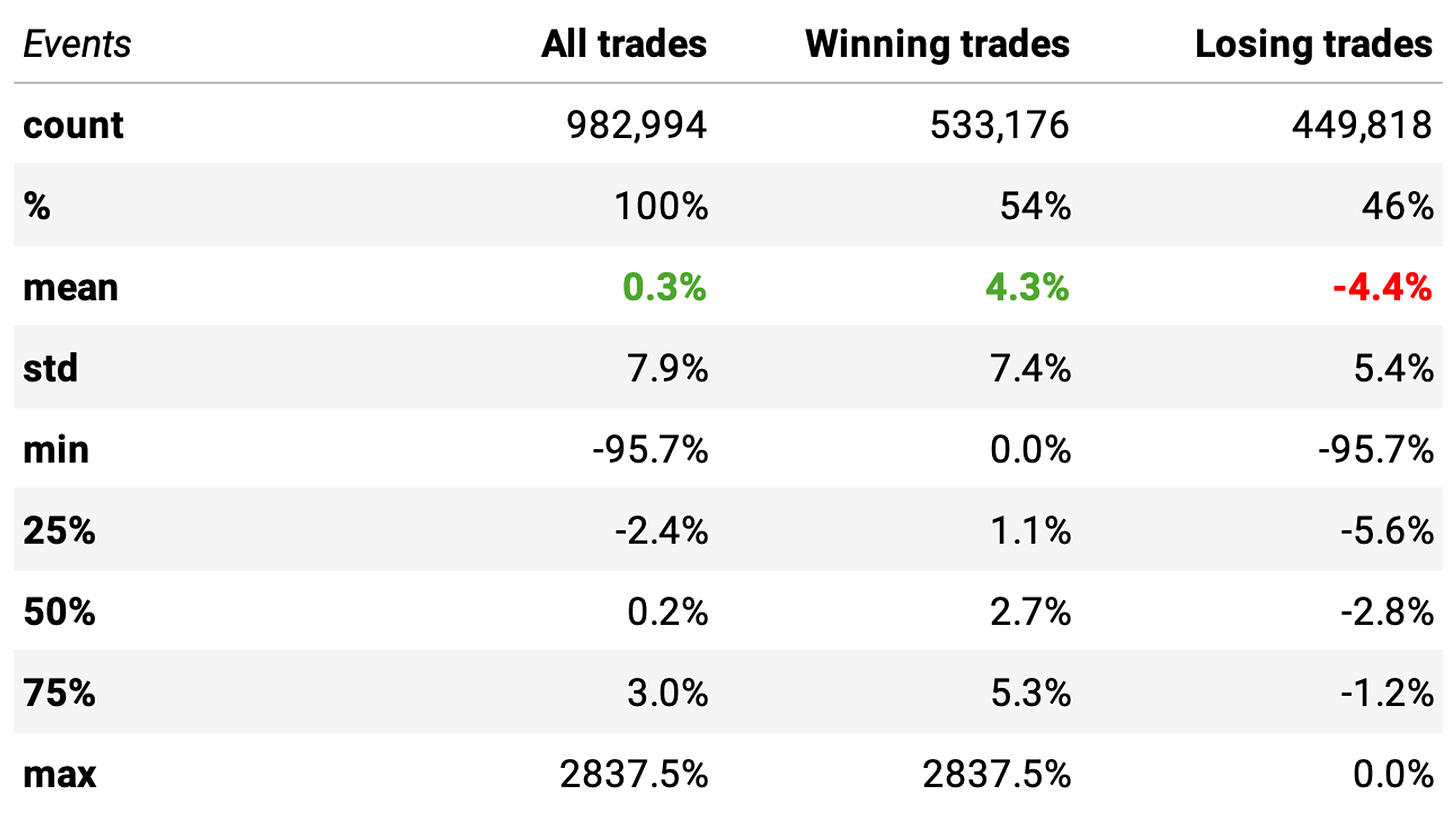
Looking at the +21K listed and delisted stocks since 1998, we see that they have triggered the strategy entry rules close to 1 million times. The results:

• The expected return is 0.3%

• The rules are better than a coin flip, with a 54% probability of success

• The payoff ratio is about 1: winning trades are expected to return 4.3%/trade while losing trades are about the same (-4.4%/trade).

Now, let's look at non-events: what would have happened if we had bought all events when a stock closed higher than the lower band or its IBS was above 0.3 and also held it for 5 days? The stats:

Statistics of non-events

Here, we see over 21 million non-events:

• The expected return is 0.0%

• The rules are closer to a fair coin flip, with a 51% probability of success

Calculating the T-test for the means of the two distributions, I found that:

• P-value is 1.3e-265 < 0.05

• ✅ The two distributions have different means with statistical significance

So, we conclude that these rules produce an edge. However, I was expecting more edge out of the strategy. Can we do something about it?

How does the edge vary with volatility?

Intuitively, I expect the edge to increase as we increase volatility. Why? Because high-volatile stocks would tend to revert to the mean sharply and faster than low-volatile stocks. I've heard this thought the other day and believe it makes sense. Let's test that.

To do it, first, we remove all events from nano, micro, small, and mid-caps. As we have seen in previous studies, these stocks have a high probability of delisting.

Then, we classify all events from mid, large and mega caps by the quintile they belong with respect to the Normalized Average True Range, which is a popular indicator of volatility. Here are the results:

Statistics of the events, by quintile of Normalized Average True Range

As expected, we do see a significant increase in expected return as we increase the volatility. The 5th quintile (the highest Normalized Average True Range) shows a 1.1% expected return.

This is driven by both an increase in % of winning trades (to 56%) and an increase in the payoff ratio (ratio between the expected return of winning trades vs. losing trades). As a result, the total expected return is 1.1% for the highest volatility bucket, over 5x higher than the lowest quintile.

How frequently do these events occur?

Finally, before we backtest the strategy, let's check how frequently these events occur:

Evolution of the number of stocks that triggered the entry rules (21-day rolling average to smooth the curve). The red line is the median value (4 stocks).

The median value of this distribution is 4: we have a sufficient number of events happening every day to devise a strategy with good exposure.

The multi-asset strategy

Now, let's define the strategy. Different than what we tested first, the strategy will trade multiple instruments in parallel to increase the exposure time. Here are the rules:

• We will split our capital into 5 slots and buy stocks that trigger the entry rule as defined in the beginning: when it closes under the lower band, and IBS is lower than 0.3, we go long at the next open;

• If there are more than 5 stocks in the universe with the entry signal triggered, we will sort them by volatility (Normalized Average True Range) and prioritize the most volatile ones;

• We will hold 5 positions maximum at any given moment;

• When the stock closes above yesterday's high, we will exit on the next open;

• Also, we will close the trade whenever the price is lower than the 200-day SMA;

• We will only trade stocks whose price is above $10 and is above its 200-day SMA.

To ensure we trade only liquid stocks:

• We will restrict ourselves to only trade stocks that have been traded in all sessions over the past 3 months from the day in question;

• We will only trade the stock if the allocated capital for the trade does not exceed 5% of the stock's median ADV of the past 3 months from the day in question.

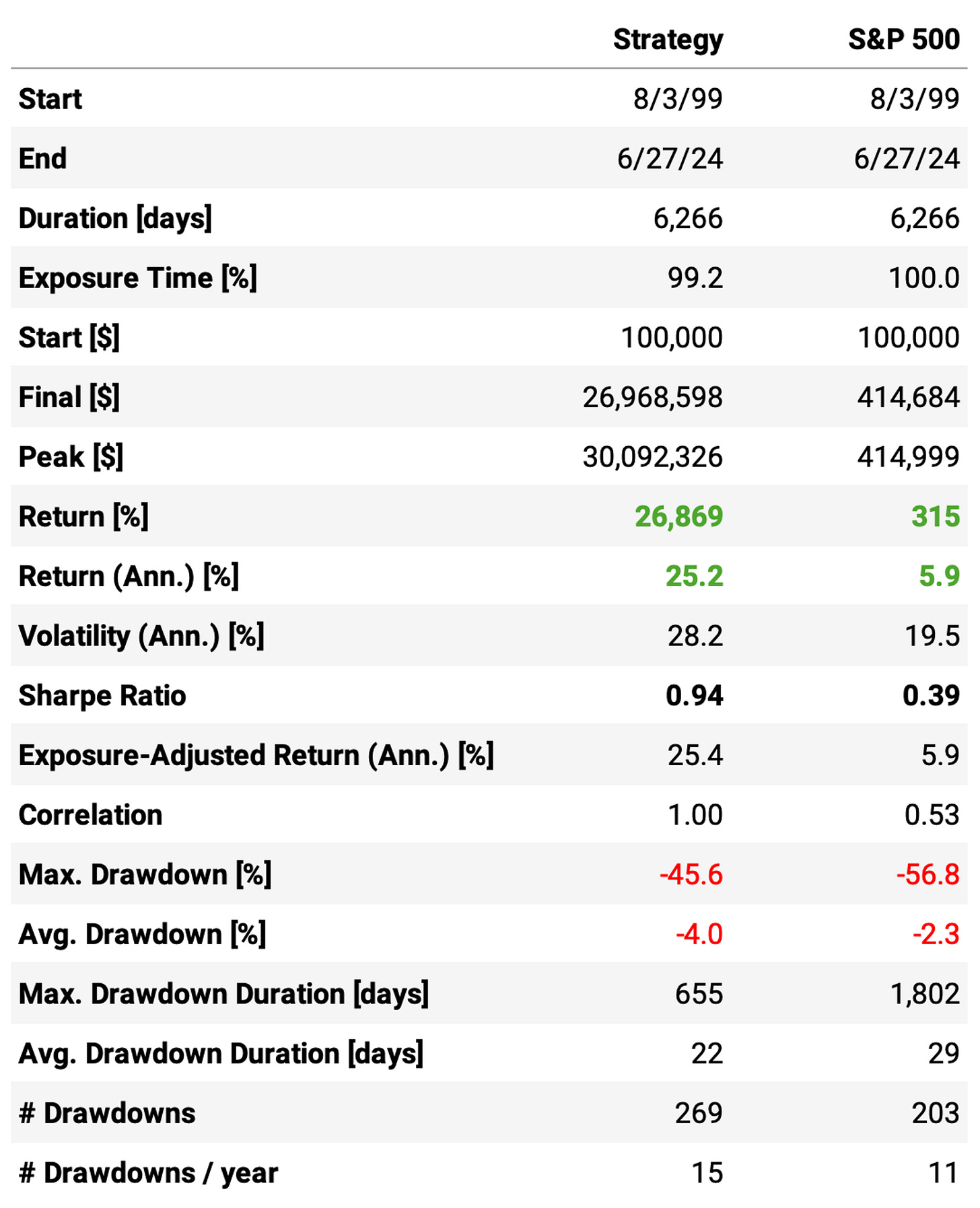
Here are the results:

Equity curve, drawdown curve, and annual returns for the multi-asset strategy

Summary of the backtest statistics

Summary of the backtest trades

That's a significantly better result than what we obtained when we traded a single instrument. The highlights:

• The annual return is 24.8%, over 2x what we had by trading only QQQ;

• The exposure time is over 99%, a stark contrast to the 22% of a single instrument;

• However, the risk-adjusted return is significantly worse: here, we achieved 0.81 Sharpe, which is better than the 0.39 Sharpe of the S&P 500 in the period but way lower than the 2.11 Sharpe we obtained when focusing only on QQQ;

• The volatility is too high, pushing the maximum drawdown to 63%.

With this level of risk, this strategy is far from ready to be traded. Few people can handle maximum drawdowns above 20%, let alone over 60%.

But what can be done to try to reduce the risk?

Diversification

Employing diversification is usually a good idea to reduce risk. So, instead of trading 5 instruments in parallel maximum, let's trade 10 and see how it impacts the numbers.

Here are the results:

Equity curve, drawdown curve, and annual returns for the multi-asset strategy, trading 10 instruments in parallel instead of 5

Summary of the backtest statistics

Summary of the backtest trades

Highlights:

• We see slight improvement in the annual return (from 24.8% to 25.2%), and also an improvement in the risk-adjusted return: Sharpe ratio goes from 0.82 to 0.94;

• The maximum drawdown reduces from 63% to 46%, better than the benchmark (57%), but still too high;

• And now, we introduce a new problem: the number of trades increase from 245/year to 487/year: this is almost 2 trades/day.

Focus on the S&P 500 constituents

We have to reduce the number of instruments traded in parallel to keep the # of trades/year to a manageable value.

So, in order to reduce the risk, let's try to focus on S&P 500 constituents. Also, we will reduce the number of trades in parallel to 3 to lower the # of trades/year.

Important: I'm using a survivorship bias-free dataset that has the S&P 500 historical constituents since 1998. If you plan to replicate this study by yourself, make sure you do not introduce survivorship bias by considering the current constituents as fixed through time.

Here are the results:

Equity curve, drawdown curve, and annual returns for the multi-asset strategy, trading 3 instruments in parallel, focusing on S&P 500 constituents

Summary of the backtest statistics

Summary of the backtest trades

Those are nice results! Highlights:

• The annual return achieved 26.4%, over 1 point above the previous result, significantly outperforming S&P 500 with over 4x its annual return;

• This new strategy also achieved the best risk-adjusted return so far, with a 0.98 Sharpe;

• The max drawdown is still high, at 46% (same as before); however, all large drawdowns are in the 1999-2013 period; the maximum drawdown over the past decade is better (<30%);

• The strategy trades 149 times/year, which is approximately 3 times/week - a more manageable value;

Final thoughts

When I start an article, I have an objective and hypothesis I want to test. But, as I never know where the numbers are going to lead me, I never know how the article is going to end. That's part of the fun of doing research.

Sometimes, an idea is easy to develop. Sometimes, it's quite hard. This article belongs to the latter group. For this to get written, I explored over 20 different directions. Finally, I'm glad I'm writing the final thoughts.

Restricting the universe to S&P 500 constituents was the key to improving the performance of this mean-reversion strategy. However, there's much more to investigate:

• Does the strategy behave differently based on the company's sectors?

• How could we play with position sizing to improve the results even further?

• How could we use leverage to accelerate the positive returns during bullish markets? (Is that even a good idea?)

• How do slippage costs impact these results (here, I'm considering a fixed 1-basis point in slippage in all transactions)?

• Could we combine it with a momentum/trend-following strategy to improve the risk-adjusted returns?

So much to do, so little time…

In the next weeks, I think I will start exploring momentum/trend-following strategies, as several people are asking me that. Thank you to all who are reaching out with ideas, comments, questions, and suggestions: developing these ideas together is much more fun!

As usual, I'd love to hear your thoughts about this approach. If you have any questions or comments, just reach out via Twitter or email.

Also, if you want to implement this strategy (or any other strategy) and need help, just let me know.

Cheers!